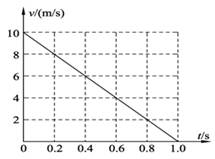
一质量m＝0.5 kg的滑块以一定的初速度冲上一倾角θ=37°足够长的斜面，某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度，并用计算机做出了小物块上滑过程的v-t图象，如图所示。（最大静摩擦力等于滑动摩擦力，取sin37°=0.6，cos37°=0.8，g="10" m/s²）求：
（1）滑块与斜面间的动摩擦因数。
（2）判断滑块最后能否返回斜面底端？若能返回，求出返回斜面底端时的速度大小；若不能返回，求出滑块停在什么位置。