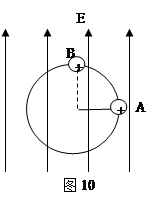
如图10所示，长L=0.20m的丝线的一端栓一质量为m=1.0×10^-4Kg带电荷量为
q=+1.0×10^-6C的小球，另一端连在一水平轴O上，丝线拉着小球可在竖直平面内做圆周运动，整个装置处在竖直向上的匀强电场中，电场强度E=2.0×10³N/C，现将小球拉到与轴O在同一水平面的A点，然后无初速地将小球释放，取g=10m/s²，求（1）小球通过最高点B时速度的大小（2）小球通过最高点时，丝线对小球的拉力大小。