（1）下列实验中，深入地揭示了光的粒子性一面的有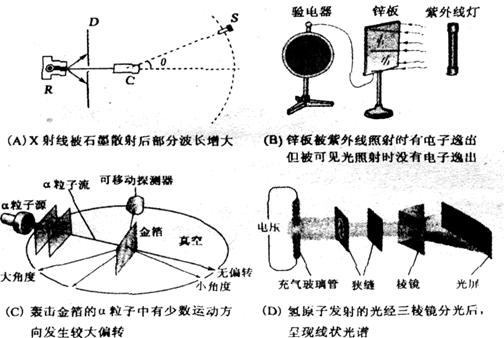
（2）铝的逸出功Wo=6．72×10-19J，现将波长λ=200nm的光照射铝的表面．求：
①光电子的最大初动能(普朗克常量h=6．63×10-34J·s)．
②若射出具有最大初动能的光电子与一静止电子发生正碰，则碰撞中两电子电势能增加的最大值是? 
相关试题
2011年9月25日，我国用长征二号F型火箭成功发射“天宫一号”目标飞行器．火箭从开始起飞到离开发射塔用时6s，假设此过程是匀加速直线运动，已知发射架高1.2×102m ，忽略空气阻力，此过程中：
(1)“天宫一号”的加速度多大；
(2)火箭离开发射架瞬间的速度．
如图所示，用细绳将重球悬挂在光滑墙壁上，绳子与墙夹角为θ，球的重力为G。
（1）用力的分解法则作出重力和重力沿绳子方向及垂直墙壁方向的两个分力
（2）这两个分力的大小是多大？
物体A在水平力F1=400N的作用下，沿倾角θ=53°的斜面匀速下滑，如图所示。物体A受的重力G=400N，求斜面对物体A的支持力和A与斜面间的动摩擦因数μ。（sin53°=0.8，cos53°=0.6）
粤公网安备 44130202000953号