如图所示,一高度为h="0.2" m的水平面在A点处与一倾角θ=30°的斜面连接,一小球以v0="5" m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g="10" m/s2).某同学对此题
的解法为:小球沿斜面运动,则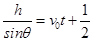 gsinθ·t2,由此可求得落地的时间t.
gsinθ·t2,由此可求得落地的时间t.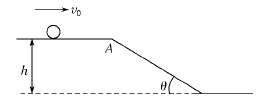
问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果.
如图所示,一高度为h="0.2" m的水平面在A点处与一倾角θ=30°的斜面连接,一小球以v0="5" m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g="10" m/s2).某同学对此题
的解法为:小球沿斜面运动,则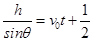 gsinθ·t2,由此可求得落地的时间t.
gsinθ·t2,由此可求得落地的时间t.
问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果.