如图所示，竖直平面内有相互垂直的匀强电场和匀强磁场，电场强度E1＝2500 N/C，方向竖直向上；磁感应强度B＝103T，方向垂直纸面向外；有一质量m＝1×10－2kg、电荷量q＝4×10－5C的带正电小球自O点沿与水平线成45°角以v0＝4 m/s的速度射入复合场中，之后小球恰好从P点进入电场强度E2＝2500 N/C，方向水平向左的第二个匀强电场中．不计空气阻力，g取10 m/s2.求：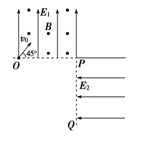
(1)O点到P点的距离s1；
(2)带电小球经过P点的正下方Q点时与P点的距离s2.
如图所示装置由AB、BC、CD三段轨道组成，轨道交接处均由很小的圆弧平滑连接，其中轨道AB、CD段是光滑的，水平轨道BC的长度
，轨道CD足够长且倾角
，A、D两点离轨道BC的高度分别为
。现让质量为m的小滑块自A点由静止释放。已知小滑块与轨道BC间的动摩擦因数为μ=0.5，重力加速度g取10m/s2，
，求：
（1）小滑块第一次到达D点时的速度大小；
（2）小滑块第一次与第二次通过C点的时间间隔；
（3）小滑块最终停止的位置距B点的距离。
如图所示，虚线上方有方向竖直向下的匀强电场，虚线上下有相同的匀强磁场，磁感应强度为B，方向垂直纸面向外，ab是一根长为
的绝缘细杆，沿电场线放置在虚线上方，b端恰在虚线上，将一套在杆上的带电量为q、质量为m的小环（小环重力忽略不计），从a端由静止释放后，小环先作加速运动，后作匀速运动到达b端，已知小环与绝缘杆间的动摩擦系数为μ，当小环脱离杆进入虚线下方后，运动轨迹是半圆，圆的半径是
，求：
（1）小环到达b点的速度
；
（2）匀强电场的场强E。
汽车发动机的额定功率为 90kW，汽车质量为3×103kg，当它沿坡度为0.04（即sinθ=0.04）的长直公路向上行驶时，所受摩擦阻力为车重的0.08倍，若汽车从静止开始以0.3m/s2的加速度沿坡路向上做匀加速直线运动，则此过程能维持多长时间？（g取10m/s2）
如图所示，足够长的光滑平行金属导轨MN、PQ竖直放置，磁感应强度B＝0.50T匀强磁场垂直穿过导轨平面，导轨的上端M与P间连接阻值为R＝0.50Ω的电阻，导轨宽度L＝0.40m。金属棒ab紧贴在导轨上，现使金属棒ab由静止开始下滑，通过传感器记录金属棒ab下滑的距离h与时间t的关系如下表所示。（金属棒ab和导轨电阻不计，g=10m/s2）
| 时 间t/s |
0 |
0.20 |
0.40 |
0.60 |
0.80 |
1.00 |
1.20 |
1.40 |
1.60 |
1.80 |
| 下滑距离h/m |
0 |
0.18 |
0.60 |
1.20 |
1.95 |
2.80 |
3.80 |
4.80 |
5.80 |
6.80 |
求：（1）在前0. 4s的时间内，金属棒ab中的平均电动势；
（2）金属棒的质量m；
（3）在前1.60s的时间内，电阻R上产生的热量QR。
粤公网安备 44130202000953号