如图所示，图甲为一个电灯两端电压与通过它的电流的变化关系曲线．由图可知，两者不成线性关系，这是由于焦耳热使灯丝的温度发生了变化的缘故，参考这条曲线回答下列问题(不计电流表内阻，线路提供电压不变)：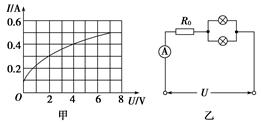
(1)若把三个这样的电灯串联后，接到电压恒定为12 V的电路上，求流过灯泡的电流和每个灯泡的电阻；
(2)如图乙所示，将两个这样的电灯并联后再与10 Ω的定值电阻R0串联，接在电压恒定为8 V的电路上，求通过电流表的电流值以及每个灯的实际功率．
如图所示，在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd，其边长为L，总电阻为R，放在磁感应强度为B．方向竖直向下的匀强磁场的左边，图中虚线MN为磁场的左边界。线框在恒力作用下向右运动，其中ab边保持与MN平行。当线框以速度v0进入磁场区域时，它恰好做匀速运动，求：
（1）线框刚进入磁场时ab边产生的感应电动势的大小为E ；
（2）在线框进入磁场的过程中a、b两点的电势差；
（3）在线框进入磁场的过程中恒力所做的功。
面积S = 0.2m2、n = 100匝的圆形线圈，处在如图所示的磁场内，磁感应强度随时间t变化的规律是B = 0.02t，R = 3Ω，C = 30μF，线圈电阻r = 1Ω，求：
（1）通过R的电流大小和方向
（2）电容器的电荷量.
如图所示，半径为r的圆形区域内存在着垂直纸面向里的匀强磁场，磁感应强度为B。现有一带电离子（不计重力）从A以速度v沿圆形区域的直径射入磁场，已知离子从C点射出磁场的方向间的夹角为60º
（1）该离子带何种电荷；
（2）求该离子的电荷量与质量之比q/m。
如图所示，水平传送带以一定速度匀速运动，将质量m=1kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、C为圆弧上的两点，其连线水平，已知圆弧对应圆心角
，A点距水平面的高度h=0.8m．小物块到达C点时的速度大小与B点相等，并沿固定斜面向上滑动，小物块从C点到第二次经过D点的时间间隔为0.8s，已知小物块与斜面间的动摩擦因数
，重力加速度g取10 m/s2，取
，cos53°=0.6，求：
（1）小物块从A到B的运动时间；
（2）小物块离开A点时的水平速度大小；
（3）斜面上C、D点间的距离．
粤公网安备 44130202000953号