在倾角为300的斜面底端,木块A以某一速度沿斜面向上运动,若木块与斜面间的动摩擦因数为 ,
,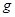 取10
取10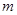 /
/ ,试求:
,试求:
(1)木块A在斜面上向上运动和向下运动的加速度各多大;
(2)木块A在斜面上离开出发点时和回到出发点时的动能之比;
(3)如在斜面底端处安装一固定且垂直于斜面的挡板,如图所示,不计物块与挡板每次碰撞的机械能损失,求物块以初速度10m/s沿斜面运动到最终停止所通过的总路程.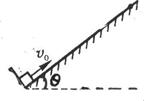
在倾角为300的斜面底端,木块A以某一速度沿斜面向上运动,若木块与斜面间的动摩擦因数为 ,
,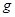 取10
取10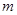 /
/ ,试求:
,试求:
(1)木块A在斜面上向上运动和向下运动的加速度各多大;
(2)木块A在斜面上离开出发点时和回到出发点时的动能之比;
(3)如在斜面底端处安装一固定且垂直于斜面的挡板,如图所示,不计物块与挡板每次碰撞的机械能损失,求物块以初速度10m/s沿斜面运动到最终停止所通过的总路程.