宇航员在某星球表面附近,距星球表面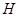 高处,静止释放一个物体,物体落到星球表面时的速度为
高处,静止释放一个物体,物体落到星球表面时的速度为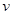 ,仅考虑物体受该星球的引力作用,忽略其他力的影响,已知该星球的直径为
,仅考虑物体受该星球的引力作用,忽略其他力的影响,已知该星球的直径为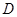 。(1)求该星球表面的重力加速度
。(1)求该星球表面的重力加速度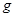 ;(2)若在该星球上发射一颗绕该星球做匀速圆周运动的卫星,卫星的高度也是
;(2)若在该星球上发射一颗绕该星球做匀速圆周运动的卫星,卫星的高度也是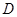 ,求这颗卫星的速度
,求这颗卫星的速度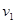 。
。
宇航员在某星球表面附近,距星球表面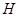 高处,静止释放一个物体,物体落到星球表面时的速度为
高处,静止释放一个物体,物体落到星球表面时的速度为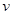 ,仅考虑物体受该星球的引力作用,忽略其他力的影响,已知该星球的直径为
,仅考虑物体受该星球的引力作用,忽略其他力的影响,已知该星球的直径为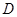 。(1)求该星球表面的重力加速度
。(1)求该星球表面的重力加速度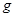 ;(2)若在该星球上发射一颗绕该星球做匀速圆周运动的卫星,卫星的高度也是
;(2)若在该星球上发射一颗绕该星球做匀速圆周运动的卫星,卫星的高度也是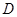 ,求这颗卫星的速度
,求这颗卫星的速度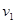 。
。