如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3秒后又恰好垂直与倾角为450的斜面相碰到。已知圆轨道半径为R=1m,小球的质量为m=1kg,g取10m/s2。求
(1)小球在斜面上的相碰点C与B点的水平距离
(2)小球经过圆弧轨道的B点时,受到轨道的作用力
NB的大小和方向?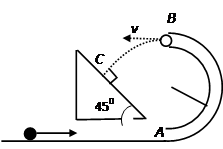
如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3秒后又恰好垂直与倾角为450的斜面相碰到。已知圆轨道半径为R=1m,小球的质量为m=1kg,g取10m/s2。求
(1)小球在斜面上的相碰点C与B点的水平距离
(2)小球经过圆弧轨道的B点时,受到轨道的作用力
NB的大小和方向?