在一真空室内存在着匀强电场和匀强磁场，电场的方向与磁场的方向相同，已知电场强度E=40.0V/m，磁感应强度B=0.30T，如图所示，在真空室内建立O—xyz三维直角坐标系，其中z轴竖直向上。质量m=1.0×10-4Kg、带负电的质点以速度v0=100m/s沿+x方向做匀速直线运动，速度方向与电场、磁场方向垂直，取g=10m/s2。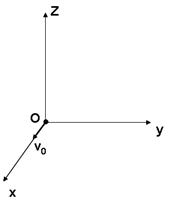
（1）求质点所受电场力与洛伦兹力的大小之比
（2）求带电质点的电荷量
（3）若在质点通过O点时撤去磁场，求经过t=0.20s时，带电质点的位置坐标。
相关试题
某汽车以20m/s的速度行驶，司机突然发现前方34m处有危险，采取制动措施。若汽车制动后做匀减速直线运动，产生的最大加速度大小为10m/s2，为保证安全，司机从发现危险到采取制动措施的反应时间不得超过多少？
如图所示，水平面上放有质量均为m＝1 kg的物块A和B(均视为质点)，A、B与地面的动摩擦因数分别为μ1＝0.4和μ2＝0.1，相距l＝0.75 m．现给物块A一初速度使之向物块B运动，与此同时给物块B一个F＝3 N水平向右的力使其由静止开始运动，经过一段时间A恰好能追上B.g＝10 m/s2.求：
(1)物块B运动的加速度大小；
(2)物块A初速度大小．
如图所示, 小车的顶棚上用绳线吊一小球, 质量为m, 车厢底板上放一个质量为M的木块, 当小车沿水平面匀加速向右运动时, 小球悬线偏离竖直方向30°, 木块和车厢保持相对静止,求：
(1)小车运动的加速度？
(2)小球对悬线的拉力？
(3)木块受到的摩擦力？
粤公网安备 44130202000953号