某滑板爱好者在离地 高的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移
高的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移 .着地时由于存在能量损失,着地后速度变为
.着地时由于存在能量损失,着地后速度变为 ,并以此为初速沿水平地面滑行
,并以此为初速沿水平地面滑行 后停止.已知人与滑板的总质量
后停止.已知人与滑板的总质量 .试求:
.试求: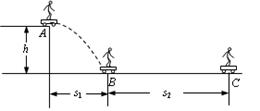
(1)人与滑板在水平地面滑行时受到的平均阻力的大小;
(2)人与滑板离开平台时的水平初速度大小(空气阻力忽略不计,取当地的重力加速度 ).
).
某滑板爱好者在离地 高的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移
高的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移 .着地时由于存在能量损失,着地后速度变为
.着地时由于存在能量损失,着地后速度变为 ,并以此为初速沿水平地面滑行
,并以此为初速沿水平地面滑行 后停止.已知人与滑板的总质量
后停止.已知人与滑板的总质量 .试求:
.试求:
(1)人与滑板在水平地面滑行时受到的平均阻力的大小;
(2)人与滑板离开平台时的水平初速度大小(空气阻力忽略不计,取当地的重力加速度 ).
).