某学习小组利用大食拉油圆桶(去掉上半部)、小石子A来测定水的折射率,如图所示。当桶内没有水时,从某点B恰能看到桶底边缘的某点C;当桶内水的深度等于桶高的一半时,仍沿BC方向看去,恰好看到桶底上的小石子A,A在圆桶的底面直径CD上。用毫米刻度尺测得直径CD=16.00cm,桶高DE=12.00cm,距离AC=3.50cm。光在真空中的传播速度为c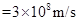 ,求水的折射率n和光在水中的传播速度v。
,求水的折射率n和光在水中的传播速度v。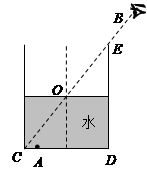
某学习小组利用大食拉油圆桶(去掉上半部)、小石子A来测定水的折射率,如图所示。当桶内没有水时,从某点B恰能看到桶底边缘的某点C;当桶内水的深度等于桶高的一半时,仍沿BC方向看去,恰好看到桶底上的小石子A,A在圆桶的底面直径CD上。用毫米刻度尺测得直径CD=16.00cm,桶高DE=12.00cm,距离AC=3.50cm。光在真空中的传播速度为c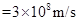 ,求水的折射率n和光在水中的传播速度v。
,求水的折射率n和光在水中的传播速度v。