2005年10月12日上午9时，“神州”六号载人飞船发射升空。 火箭点火起飞，588秒后，飞船与火箭分离，准确入轨，进入椭圆轨道运行。飞船飞行到第5圈实施变轨，进入圆形轨道绕地球飞行。设“神州”六号飞船质量为m，当它在椭圆轨道上运行时，其近地点距地面高度为h1，飞船速度为v1，加速度为a1；在远地点距地面高度为h2，飞船速度为v2.已知地球半径为R（如图所示）。求飞船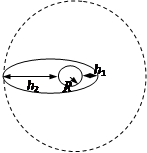
（1）由远地点到近地点万有引力所做的功
（2）在远地点的加速度a2
如图，质量m=2kg的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经t0=2s拉至B处。(已知cos370=0.8,sin370=0.6。取g=10m/s2)
(1)求物体与地面间的动摩擦因数μ；
(2)用大小为30N，与水平方向成37°的力斜向上拉此物体，使物体从A处由静止开始运动并能到达B处，求该力作用的最短时间t。
如图所示，一个质量为0.6 kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)．已知圆弧的半径R＝0.3 m，θ＝60°，小球到达A点时的速度vA＝4 m/s.(取g＝10 m/s2)求：
(1)小球做平抛运动的初速度v0；
(2)P点到A点的水平距离和竖直距离；
(3)小球到达圆弧最高点C时对轨道的压力．
如图所示，绷紧的传送带与水平面的夹角θ=30°，皮带在电动机的带动下，始终保持V0=2m/s的速率顺时针运行。现把一质量m=10kg的工件（可看为质点）轻轻放在皮带的底端，经时间t=1.9s，工件被传送到h=1.5m的高处，取g=10m/s2.
求（1）工件与皮带间的动摩擦因数。
（2）电动机由于传送工件多消耗的电能。
如图所示，跨过同一高度处的光滑滑轮的细线连接着质量相同的物体A和B。A套在光滑水平杆上，定滑轮离水平杆高度为h="0.2" m。开始让连A的细线与水平杆夹角θ=53°，由静止释放，求在以后的过程中A所能获得的最大速度。
（已知cos53°=0.6，sin53°=0.8，g="10" m/s2）
g=5m/s2的加速度匀加速上升，由于超重现象，用弹簧秤测得质量为10kg的物体重量为75N，由此可求飞船所处位置距地面高度为多少？(地球半径R=6400km)
粤公网安备 44130202000953号