如图所示，在矩形ABCD区域内，对角线BD以上的区域存在有平行于AD向下的匀强电场，对角线BD以下的区域存在有垂直于纸面的匀强磁场（图中未标出），矩形AD边长为L，AB边长为2L。一个质量为m、电荷量为+q的带电粒子（重力不计）以初速度v0从A点沿AB方向进入电场，在对角线BD的中点P处进入磁场，并从DC边上以垂直于DC边的速度离开磁场（图中未画出），求：
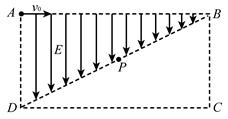
（1）电场强度E的大小和带电粒子经过P点时速度v的大小和方向；
（2）磁场的磁感应强度B的大小和方向。
如图甲所示，光滑绝缘水平面上，磁感应强度B=2T的匀强磁场以虚线MN为左边界，MN的左侧有一质量m=0.1kg，bc边长L1=0.2m，电阻R=2Ω的矩形线圈abcd．t=0时，用一恒定拉力F拉线圈，使其由静止开始向右做匀加速运动，经过时间1s，线圈的bc边到达磁场边界MN，此时立即将拉力F改为变力，又经过1s，线圈恰好完全进入磁场．整个运动过程中，线圈中感应电流i随时间t变化的图象如图乙所示．
（1）求线圈bc边刚进入磁场时的速度v1和线圈在第ls内运动的距离x；
（2）写出第2s内变力F随时间t变化的关系式；
（3）求出线圈ab边的长度L2．
如图所示，一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场，在ad边中点O，方向垂直磁场向里射入一速度方向跟ad边夹角θ=30°、大小为v0的带正电粒子，已知粒子质量为m，电量为q，ad边长为L，ab边足够长，粒子重力不计，求：
（1）粒子能从ab边上射出磁场的v0大小范围．
（2）如果带电粒子不受上述v0大小范围的限制，求粒子在磁场中运动的最长时间．
有一金属细棒ab，质量m=0.05kg，电阻不计，可在两条轨道上滑动，如图所示，轨道间距为L=0.5m，其平面与水平面的夹角为θ=37°，置于垂直于轨道平面向上的匀强磁场中，磁感应强度为B=1.0T，金属棒与轨道的动摩擦因数μ=0.5，（设最大静摩擦力与滑动摩擦力大小相等）回路中电源电动势为E=3V，内阻r=0.5Ω．求：
①为保证金属细棒不会沿斜面向上滑动，流过金属细棒ab的电流的最大值为多少？
②滑动变阻器R的阻值应调节在什么范围内，金属棒能静止在轨道上？
（g=10m/s2，sin37°=0.6，cos37°=0.8）
有一带电量q=﹣3×10﹣6C的点电荷，从电场中的A点移到B点时，克服电场力做功6×10﹣4J，从B点移到C点时电场力做功9×10﹣4J．问：
（1）AB、BC、CA间电势差各为多少？
（2）如以B点为零电热，则A、C两点的电势各为多少？
，cos60°=
）
粤公网安备 44130202000953号