如图所示，倾角为θ=30°的足够长的固定斜面上，在底端0处固定一垂直斜面的档板，斜面上OM段光滑，M点及以上均粗糙。质量为m的物块A在M点恰好能静止，有一质量为2m的光滑小物块B以初速度
自N点滑向物块A，已知MN=L，AB间每次碰撞后即紧靠在一起但不粘连，每次AB与档板碰撞后均原速率弹回，求：
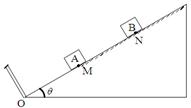
(1)A、B第一次碰撞后紧靠在一起的初速度
；
(2)物块A在M点上方时，离M点的最大距离s；
(3)系统由于摩擦和碰撞所产生的总内能E。
物体A的质量为mA，圆环B的质量为mB，通过绳子连接在一起，圆环套在光滑的竖直杆上，开始时连接圆环的绳子处于水平，如图所示，长度l＝4 m，现从静止释放圆环．不计定滑轮和空气的阻力，取g＝10 m/s2，求：
(1)若
，则圆环能下降的最大距离hm；
(2)若圆环下降h2＝3 m时的速度大小为4 m/s，则两个物体的质量应满足怎样的关系？
(3)若
，请定性说明小环下降过程中速度大小变化的情况及其理由。
如图所示，倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内．一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑并进入圆环轨道．接着小滑块从圆环最高点C水平飞出，恰好击中导轨上与圆心O等高的P点，不计空气阻力．求：
（1）滑块运动到圆环最高点C时的速度的大小；
（2）滑块运动到圆环最低点时对圆环轨道压力的大小；
（3）滑块在斜面轨道BD间运动的过程中克服摩擦力做的功。
如图所示，轨道ABCD的AB段为一半径R=0.2m的光滑 1/4 圆形轨道，BC段为高为h=5m的竖直轨道，CD段为水平轨道．一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s，离开B点做平抛运动（g取10m/s2），求：
（1）小球离开B点后，在CD轨道上的落地点到C的水平距离；
（2）小球到达B点时对圆形轨道的压力大小？
（3）如果在BCD轨道上放置一个倾角θ=45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置．
某星球半径为R = 6
106 m，假设该星球表面上有一倾角为θ = 30°的固定斜面，一质量为m =" 1" kg的小物块在力，作用下从静止开始沿斜面向上运动，力F始终与斜面平行，如图甲所示。已知小物块和斜面间的动摩擦因数
，力F随位移x变化的规律如图乙所示（取沿斜面向上的方向为正向），如果小物块运动12 m时速度恰好为零，已知万有引力常量G = 6.6710-11 N·m2/kg2。试求：（计算结果保留一位有效数字）
（1）该星球表面上的重力加速度g的大小；
（2）该星球的平均密度。
粤公网安备 44130202000953号