如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内做圆周运动,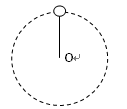
(1)小球在最高点的速度大小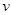 至少为多少才能顺利通过最高点?
至少为多少才能顺利通过最高点?
(2)当小球在最高点速度为4m/s时,细线的拉力F的大小为多少?
(3)此后小球运动到最低点时速度大小 ,若在最低点时细线刚好断掉,则小球落地时距O点的水平距离是多少?(已知O点离地高
,若在最低点时细线刚好断掉,则小球落地时距O点的水平距离是多少?(已知O点离地高 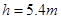 ,
,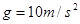 )
)
如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内做圆周运动,
(1)小球在最高点的速度大小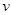 至少为多少才能顺利通过最高点?
至少为多少才能顺利通过最高点?
(2)当小球在最高点速度为4m/s时,细线的拉力F的大小为多少?
(3)此后小球运动到最低点时速度大小 ,若在最低点时细线刚好断掉,则小球落地时距O点的水平距离是多少?(已知O点离地高
,若在最低点时细线刚好断掉,则小球落地时距O点的水平距离是多少?(已知O点离地高 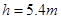 ,
,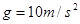 )
)