如图所示,将质量为m=1kg的小物块放在半圆形轨道最低点M左侧的A处,AM距离为L=1.5m,物块与地面间的动摩擦因数μ=0.5,半圆形轨道直径 d=1.8m;固定在水平面上,且直径 MON竖直,现物块以10m/s的初速度在水平地面上向右运动,求:
(1)小物块到达M时的速度。
(2)受上升过程中摩擦阻力影响,小物块刚好能到达轨道最高点N。求小物块落地点到M的水平距离。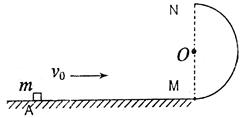
如图所示,将质量为m=1kg的小物块放在半圆形轨道最低点M左侧的A处,AM距离为L=1.5m,物块与地面间的动摩擦因数μ=0.5,半圆形轨道直径 d=1.8m;固定在水平面上,且直径 MON竖直,现物块以10m/s的初速度在水平地面上向右运动,求:
(1)小物块到达M时的速度。
(2)受上升过程中摩擦阻力影响,小物块刚好能到达轨道最高点N。求小物块落地点到M的水平距离。