如图所示的空间分布I、Ⅱ、Ⅲ、Ⅳ四个区域,各边界面相互平行,I区域存在匀强电场,电场强度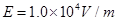 ,方向垂直边界面向右.Ⅱ、Ⅳ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为
,方向垂直边界面向右.Ⅱ、Ⅳ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为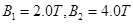 ,Ⅲ区域内无电磁场。四个区域宽度分别为
,Ⅲ区域内无电磁场。四个区域宽度分别为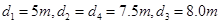 .一质量
.一质量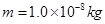 、电荷量
、电荷量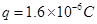 的粒子从O点由静止释放,粒子的重力忽略不计.
的粒子从O点由静止释放,粒子的重力忽略不计.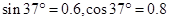 求:
求:粒子离开I区域时的速度大小v;
粒子在Ⅲ区域内运动时间t;
(此问省示范高中学生必做,其他学校学生不做)粒子离开区域Ⅳ时速度与磁场边界面的夹角α.
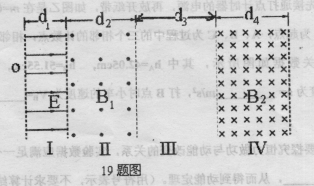
如图所示的空间分布I、Ⅱ、Ⅲ、Ⅳ四个区域,各边界面相互平行,I区域存在匀强电场,电场强度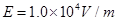 ,方向垂直边界面向右.Ⅱ、Ⅳ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为
,方向垂直边界面向右.Ⅱ、Ⅳ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为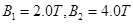 ,Ⅲ区域内无电磁场。四个区域宽度分别为
,Ⅲ区域内无电磁场。四个区域宽度分别为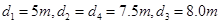 .一质量
.一质量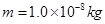 、电荷量
、电荷量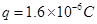 的粒子从O点由静止释放,粒子的重力忽略不计.
的粒子从O点由静止释放,粒子的重力忽略不计.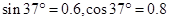 求:
求:粒子离开I区域时的速度大小v;
粒子在Ⅲ区域内运动时间t;
(此问省示范高中学生必做,其他学校学生不做)粒子离开区域Ⅳ时速度与磁场边界面的夹角α.
