如图所示,一平行板电容器水平放置,两板有方向竖直向上的匀强电场,板间距d=0.40m,电压U=10V,金属板M上开有一小孔。有A、B两个质量均为m=0.10g、电荷量均为q=+8.0×10-5C的带电小球(可视为质点),其间用长为L=0.10m的绝缘轻杆相连,处于竖直状态,A小球恰好位于小孔正上方H=0.20m处。现由静止释放并让两个带电小球保持竖直下落,(g取10m/s2)
求小球在运动过程中的最大速率。
小球在运动过程中距N板的最小距离。
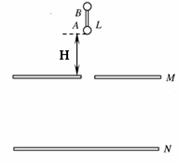
如图所示,一平行板电容器水平放置,两板有方向竖直向上的匀强电场,板间距d=0.40m,电压U=10V,金属板M上开有一小孔。有A、B两个质量均为m=0.10g、电荷量均为q=+8.0×10-5C的带电小球(可视为质点),其间用长为L=0.10m的绝缘轻杆相连,处于竖直状态,A小球恰好位于小孔正上方H=0.20m处。现由静止释放并让两个带电小球保持竖直下落,(g取10m/s2)
求小球在运动过程中的最大速率。
小球在运动过程中距N板的最小距离。
