如图所示,水平面上有两根光滑金属导轨平行固定放置,导轨的电阻不计,间距为l =" O.5" m,左端通过导线与阻值R =3Ω的电阻连接,右端通过导线与阻值为RL=6Ω的小灯泡L连接,在CDEF矩形区域内有竖直向上,磁感应强度B = O.2T的匀强磁场。一根阻值r =O.5Ω、质量m = O.2kg的金属棒在恒力F ="2" N的作用下由静止开始从AB位置沿导轨向右运动,经过t ="1" s刚好进入磁场区域。求金属棒刚进入磁场时:
金属棒切割磁场产生的电动势;
小灯泡两端的电压和金属棒受安培力。
相关知识点
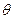 =30°角,上端连接
=30°角,上端连接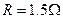 的电阻.质量为m=0.2kg、阻值
的电阻.质量为m=0.2kg、阻值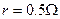 的金属棒ab放在两导轨上,与导轨垂直并接触良好,距离导轨最上端d=4m,整个装置处于匀强磁场中,磁场的方向垂直导轨平面向上.
的金属棒ab放在两导轨上,与导轨垂直并接触良好,距离导轨最上端d=4m,整个装置处于匀强磁场中,磁场的方向垂直导轨平面向上.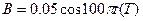 ,在平行于导轨平面的外力F作用下ab棒保持静止,求此外力F的大小范围.
,在平行于导轨平面的外力F作用下ab棒保持静止,求此外力F的大小范围.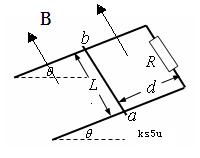


 、宽
、宽 的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。
的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。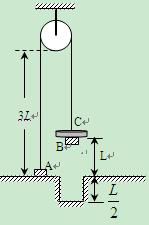
 射入,所有粒子在AB间的飞行时间均为T,不计重力影响。
射入,所有粒子在AB间的飞行时间均为T,不计重力影响。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号