现有两个宽度为d、质量为m的相同的小物块A、B,一带孔圆环C,其质量为2m,半径为d,它们的厚度均可忽略。一不可伸长的轻质细绳绕过光滑的定滑轮,一端连接A物块,一端穿过圆环C的小孔连接B物块,如图所示。现将A置于水平地面,距滑轮底端3L,BC距水平地面为L,在B的正下方有一深 、宽
、宽 的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。
的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。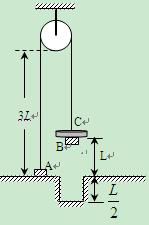
现有两个宽度为d、质量为m的相同的小物块A、B,一带孔圆环C,其质量为2m,半径为d,它们的厚度均可忽略。一不可伸长的轻质细绳绕过光滑的定滑轮,一端连接A物块,一端穿过圆环C的小孔连接B物块,如图所示。现将A置于水平地面,距滑轮底端3L,BC距水平地面为L,在B的正下方有一深 、宽
、宽 的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。
的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。