如图所示,地面和半圆轨道面均光滑。质量M=1kg、长L=4m的小车放在地面上,其右端与墙壁距离为S,小车上表面与半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(不计大小)以v0=6m/s的初速度滑上小车左端,带动小车向右运动。小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数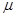 =0.2,g取m/s2。
=0.2,g取m/s2。求小车与墙壁碰撞时的速度;
要滑块能沿圆轨道运动而不脱离圆轨道,求半圆轨道的半径R的取值。
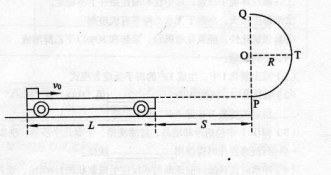
如图所示,地面和半圆轨道面均光滑。质量M=1kg、长L=4m的小车放在地面上,其右端与墙壁距离为S,小车上表面与半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(不计大小)以v0=6m/s的初速度滑上小车左端,带动小车向右运动。小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数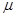 =0.2,g取m/s2。
=0.2,g取m/s2。求小车与墙壁碰撞时的速度;
要滑块能沿圆轨道运动而不脱离圆轨道,求半圆轨道的半径R的取值。
