在半径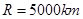 的某星球表面,宇航员做了如下实验,实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量
的某星球表面,宇航员做了如下实验,实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量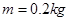 的小球从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应F的大小,F随H的变化如图乙所示。求:
的小球从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应F的大小,F随H的变化如图乙所示。求:
圆轨道的半径。
该星球表面的重力加速度多大。
该星球的第一宇宙速度。
在半径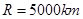 的某星球表面,宇航员做了如下实验,实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量
的某星球表面,宇航员做了如下实验,实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量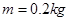 的小球从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应F的大小,F随H的变化如图乙所示。求:
的小球从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应F的大小,F随H的变化如图乙所示。求:
圆轨道的半径。
该星球表面的重力加速度多大。
该星球的第一宇宙速度。