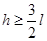如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),小球通过最低点时的速度为v。求小球通过最低点时,绳对小球拉力F的大小;
若小球运动到最低点或最高点时,绳突然断开,两种情况下小球从抛出到落地水平位移大小相等,求O点距地面的高度h;
在(2)中所述情况下试证明O点距离地面高度h与绳长l之间应满足
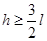
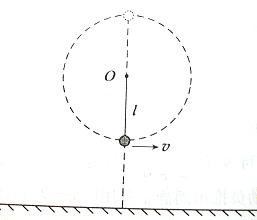
如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),小球通过最低点时的速度为v。求小球通过最低点时,绳对小球拉力F的大小;
若小球运动到最低点或最高点时,绳突然断开,两种情况下小球从抛出到落地水平位移大小相等,求O点距地面的高度h;
在(2)中所述情况下试证明O点距离地面高度h与绳长l之间应满足