用四个阻值均为R的电阻连成如图所示的电路,开关S闭合时,有一质量为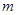 ,带电荷量为
,带电荷量为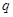 的小球静止于水平放置的平行板电容器的中点,平行板电容器的下极板接地。现打开开关S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电荷量发生变化,碰后小球带有和该极板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为
的小球静止于水平放置的平行板电容器的中点,平行板电容器的下极板接地。现打开开关S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电荷量发生变化,碰后小球带有和该极板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为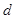 ,不计电源内阻,求:
,不计电源内阻,求: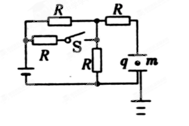
小球开始带什么电?小球开始在中点的电势是多少?电源电动势E为多大?
小球与极板碰撞后所带的电荷量
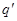 为多少?
为多少?
用四个阻值均为R的电阻连成如图所示的电路,开关S闭合时,有一质量为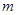 ,带电荷量为
,带电荷量为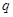 的小球静止于水平放置的平行板电容器的中点,平行板电容器的下极板接地。现打开开关S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电荷量发生变化,碰后小球带有和该极板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为
的小球静止于水平放置的平行板电容器的中点,平行板电容器的下极板接地。现打开开关S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电荷量发生变化,碰后小球带有和该极板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为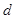 ,不计电源内阻,求:
,不计电源内阻,求:
小球开始带什么电?小球开始在中点的电势是多少?电源电动势E为多大?
小球与极板碰撞后所带的电荷量
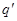 为多少?
为多少?