如图所示,1、2两细绳与水平车顶的夹角分 别为300和600,物体质量为m,现让小车以2g(g为重力加速度)的加速度向右做匀加速直线运动,当物体与车保持相对静止时,求:绳1中弹力的大小?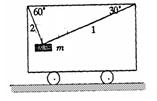
下面是一位同学的解法
解:以物体m为研究对象,受力分析如图,由牛顿第二定律得:
x:T1cos300-T2cos600=ma
y:T1sin300 +T2sin600=mg
解得: T1=(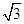 +
+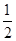 )mg
)mg
你认为该同学的解法正确吗?如有错误请写出正确的解法。
如图所示,1、2两细绳与水平车顶的夹角分 别为300和600,物体质量为m,现让小车以2g(g为重力加速度)的加速度向右做匀加速直线运动,当物体与车保持相对静止时,求:绳1中弹力的大小?
下面是一位同学的解法
解:以物体m为研究对象,受力分析如图,由牛顿第二定律得:
x:T1cos300-T2cos600=ma
y:T1sin300 +T2sin600=mg
解得: T1=(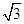 +
+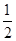 )mg
)mg
你认为该同学的解法正确吗?如有错误请写出正确的解法。