一学生用弹簧秤竖直悬挂质量为m的砝码，由静止乘电梯从地面到达某楼层，同时不断地观察弹簧秤示数的变化，记下相应的数据和时间，根据所得数据绘出了如图所示的v-t图象．试求：(取重力加速度g为10 m／S2)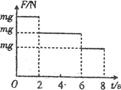
电梯运行中的最大速度
电梯上升的最大高度．
相关试题
(10分)做匀变速直线运动的质点，它在第2秒末的速度为4m/s，在第3秒末的速度为6m/s，求：（1）它的加速度为多少？
（2）它的初速度为多少？
（3）它在第3秒内的位移为多少？
长为L的平行金属板，板门形成匀强电场，一个带电为＋q、质量为m的带电粒子（不计重力），以初速v0紧贴上板垂直于电场线方向射入该电场，刚好从下板边缘射出，末速度恰与下板成30°，如图所示．
求：（1）粒子离开电场时速度的大小V．
（2）匀强电场的场强．
（3）两板间的距离d．
一个灯泡L，额定电压U=6V、额定功率P=12W。一台直流电动机D，其线圈电阻R=2Ω，把L与D并联，当电动机正常丁作时，灯泡也正常发光。如果把L与D串联，当电动机正常工作时，灯泡的实际功率是P1 =9W.求这时电动机转化为机械能的功率(假定灯泡电阻保持不变).
粤公网安备 44130202000953号