一颗在赤道上空飞行的人造地球卫星, 其轨道半径为r =3R(R为地球半径), 已知地球表面重力加速度为g,则:
(1)该卫星的运行周期是多大?
(2)若卫星的运动方向与地球自转方向相同, 已知地球自转角速度为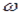 0,某一时刻该卫星通过赤道上某建筑物的正上方, 它下一次出现在该建筑物正上方经过多少时间?
0,某一时刻该卫星通过赤道上某建筑物的正上方, 它下一次出现在该建筑物正上方经过多少时间?
一颗在赤道上空飞行的人造地球卫星, 其轨道半径为r =3R(R为地球半径), 已知地球表面重力加速度为g,则:
(1)该卫星的运行周期是多大?
(2)若卫星的运动方向与地球自转方向相同, 已知地球自转角速度为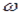 0,某一时刻该卫星通过赤道上某建筑物的正上方, 它下一次出现在该建筑物正上方经过多少时间?
0,某一时刻该卫星通过赤道上某建筑物的正上方, 它下一次出现在该建筑物正上方经过多少时间?