如图所示,质量为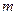 、电荷量为
、电荷量为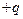 的带电小球拴在一不可伸长的绝缘轻细绳一端,绳的另一端固定于
的带电小球拴在一不可伸长的绝缘轻细绳一端,绳的另一端固定于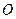 点,绳长为
点,绳长为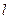 。现加一个水平向右的匀强电场,小球静止于与竖直方向成
。现加一个水平向右的匀强电场,小球静止于与竖直方向成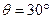 角的A点。已知重力加速度为
角的A点。已知重力加速度为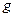 。
。
求:(1)所加电场的场强E的大小;
(2)若将小球拉起至与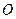 点等高的B点后无初速释放,则小球经过最低点C时,绳对小球拉力的大小。
点等高的B点后无初速释放,则小球经过最低点C时,绳对小球拉力的大小。
如图所示,质量为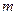 、电荷量为
、电荷量为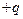 的带电小球拴在一不可伸长的绝缘轻细绳一端,绳的另一端固定于
的带电小球拴在一不可伸长的绝缘轻细绳一端,绳的另一端固定于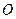 点,绳长为
点,绳长为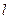 。现加一个水平向右的匀强电场,小球静止于与竖直方向成
。现加一个水平向右的匀强电场,小球静止于与竖直方向成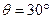 角的A点。已知重力加速度为
角的A点。已知重力加速度为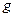 。
。
求:(1)所加电场的场强E的大小;
(2)若将小球拉起至与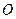 点等高的B点后无初速释放,则小球经过最低点C时,绳对小球拉力的大小。
点等高的B点后无初速释放,则小球经过最低点C时,绳对小球拉力的大小。