如图所示,长为L(L=ab=dc),高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场。电量为q、质量为m、初速度为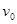 的带电粒子从a点沿ab方向进入电场,不计粒子重力。
的带电粒子从a点沿ab方向进入电场,不计粒子重力。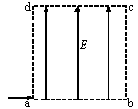
(1)若粒子从c点离开电场,求电场强度的大小
(2)若粒子从bc边某处离开电场时速度为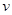 ,求电场强度的大小
,求电场强度的大小
(3) 若粒子从cd边某处离开电场时速度为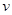 ,求电场强度的大小
,求电场强度的大小
如图所示,长为L(L=ab=dc),高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场。电量为q、质量为m、初速度为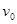 的带电粒子从a点沿ab方向进入电场,不计粒子重力。
的带电粒子从a点沿ab方向进入电场,不计粒子重力。
(1)若粒子从c点离开电场,求电场强度的大小
(2)若粒子从bc边某处离开电场时速度为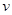 ,求电场强度的大小
,求电场强度的大小
(3) 若粒子从cd边某处离开电场时速度为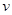 ,求电场强度的大小
,求电场强度的大小