高温超导限流器由超导部件和限流电阻并联组成，如图所示。其中的超导部件有一个超导临界电流IC，当通过限流器的电流I>IC时，将造成超导体失超，即从超导态（电阻为零）转变成正常态（成为一个普通电阻），以此来限制电力系统的故障电流。已知超导部件成正常态时的电阻R1=3Ω，超导临界电流IC=1.2A，限流电阻R2=6Ω，小灯泡上标有“6V，6W”的字样，电源电动势E=8V，内阻r=2Ω，此时电路正常工作。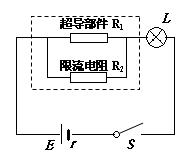
问：（1）求此时通过限流电阻R2的电流为多大；
（2）若L突然发生短路，则流过R2的电流为多大。
相关试题
已知某金属表面接受波长为λ和2λ的单色光照射时，释放出光电子的最大初动能分别为30 eV和10 eV，求能使此种金属表面产生光电效应的入射光的极限波长为多少？(λ为未知量)
氢原子光谱除了巴耳末系外，还有赖曼系、帕邢系等，其中帕邢系的公式为
＝
R(
－
)(n＝4,5,6，…)，R＝1.10×107 m－1.若已知帕邢系的氢原子光谱在红外线区域，试求：
(1)n＝6时，对应的波长；
(2)帕邢系形成的谱线在真空中的波速为多少？n＝6时，传播频率为多大？
氢原子第n能级的能量为En＝
，其中E1是基态能量，而n＝1,2，…，若一氢原子发射能量为－
E1的光子后处于比基态能量高出－
E1的激发态，则氢原子发射光子前、后分别处于第几能级？
粤公网安备 44130202000953号