如图所示，足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场，现从ad边的中心O点处，垂直磁场方向射入一速度为v0的带正电粒子，v0与ad边的夹角为30°.已知粒子质量为m，带电量为q，ad边长为L，不计粒子的重力.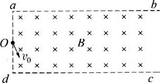
求要使粒子能从ab边射出磁场，v0的大小范围.
粒子在磁场中运动的最长时间是多少?在这种情况下，粒子将从什么范围射出磁场?
如图所示，光滑斜面的倾角
=30°，在斜面上放置一矩形线框abcd，ab边的边长l1=lm，bc边的边长l2=0.6m，线框的质量m=1kg，电阻R=0.1Ω，线框受到沿光滑斜面向上的恒力F的作用，已知F=10N．斜面上ef线（ef∥gh）的右方有垂直斜面向上的均匀磁场，磁感应强度B随时间t的变化情况如B-t图象，时间t是从线框由静止开始运动时刻起计的．如果线框从静止开始运动，进入磁场最初一段时间是匀速的，ef线和gh的距离s=5.1m，求：
（1）线框进入磁场时匀速运动的速度v；
（2）ab边由静止开始到运动到gh线处所用的时间t；
（3）线框由静止开始到运动到gh线的整个过程中产生的焦耳热
(16分）滑跃式甲板是航母比较常用的一种形式，是蒸汽弹射器的一种替代方案，主要借由甲板前端的上翘来帮助战斗机起飞,包括跑道部分和滑跃甲板部分，我国的航母训练舰就是采用滑跃式甲板.如图所示，设某航空母舰上的起飞跑道由长度为l1=1.6×102m的水平跑道和长度为l2=20m的倾斜跑道两部分组成.水平跑道与倾斜跑道末端的高度差h=4.0m.—架质量为m=2。0×104kg的飞机，其喷气发动机的推力大小恒为F=1.2×105N，方向与速度方向相同，在运动过程中飞机受到跑道与空气的平均阻力大小为飞机重力的0.1倍.假设航母处于静止状态，飞机质量视为不变并可看成质点，取g = 10m/s2.(不计拐角处的影响）求：
(1)飞机在水平跑道末端时推力的功率；
(2) 飞机到达倾斜跑道末端时的速度大小.
如图甲所示，在xOy坐标平面的第一象限（包括x、y轴）内存在磁感应强度大小为B0、方向垂直于xOy平面且随时间做周期性变化的匀强磁场，如图乙所示，规定垂直xOy平面向里的磁场方向为正。在y轴左侧有一对竖直放置的平行金属板M、N，两板间的电势差为U0。一质量为m、电量为q的带正电粒子（重力和空气阻力均忽略不计），从贴近M板的中点无初速释放，通过N板小孔后从坐标原点O以某一速度沿x轴正方向垂直射入磁场中，经过一个磁场变化周期T0（T0未知）后到达第一象限内的某点P，此时粒子的速度方向恰好沿x轴正方向。
（1）求粒子进入磁场作匀速圆周运动时的运动半径；
（2）若粒子在t=0时刻从O点射入磁场中，求粒子在P点纵坐标的最大值ym及相应的磁场变化周期T0的值；
（3）若在上述（2）中，第一象限内y=ym处平行x轴放置有一屏幕，如图甲，磁场变化周期为上述（2）中T0，但M、N两板间的电势差U可以在U0<U<9U0范围内变化，粒子仍在t=0时刻从O点射入磁场中，求粒子可能击中的屏幕范围。
在水平方向的匀强电场中有一段表面光滑的圆形绝缘杆ABC、圆心为O点，半径为R=
m， A、O两点等高，C、O两点的连线与竖直方向成θ=45°角C点到斜面的距离L=
m，斜面倾角为α=45°，如图所示。有一质量m=" 500" g的带负电小环套在直杆上，所受电场力的大小等于其重力大小，小环由A点静止开始沿杆下滑，飞出C点后撞上斜面某点。（已知
≈1.4，g取10 m／s2）求：
（1）小环到C点的速度大小；
（2）小环由C点抛出到撞击斜面所经历的时间和撞击点与C点的距离。（保留两位有效数字）
粤公网安备 44130202000953号