如图所示,在竖直平面内,光滑绝缘直杆与半径为R的圆周交于B、C两点,在圆心处有一固定的正点电荷,B点为AC的中点,C点位于圆周的最低点。现有一质量为m、电荷量为-q、套在杆上的带负电荷小球(可视为质点)从A点由静止开始沿杆下滑。已知重力加速度为g,A点距过C点的水平面的竖直高度为3R,小球滑到B点时的速度大小为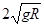 。求:
。求: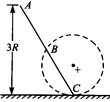
小球滑至C点时的速度的大小;
A、B两点间的电势差;
若以C点作为参考点(零电势点),试确定A点的电势.
如图所示,在竖直平面内,光滑绝缘直杆与半径为R的圆周交于B、C两点,在圆心处有一固定的正点电荷,B点为AC的中点,C点位于圆周的最低点。现有一质量为m、电荷量为-q、套在杆上的带负电荷小球(可视为质点)从A点由静止开始沿杆下滑。已知重力加速度为g,A点距过C点的水平面的竖直高度为3R,小球滑到B点时的速度大小为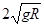 。求:
。求:
小球滑至C点时的速度的大小;
A、B两点间的电势差;
若以C点作为参考点(零电势点),试确定A点的电势.