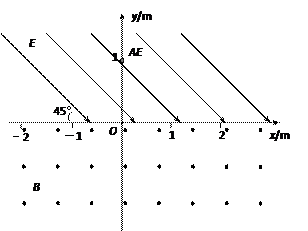
 在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=
在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E= ×104V/m。x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为 B=1×10-2T。把一个比荷为
×104V/m。x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为 B=1×10-2T。把一个比荷为 C/kg的正电荷从y轴上坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计,求:
C/kg的正电荷从y轴上坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计,求:
(1)电荷从释放到第一次进入磁场时所用的时间t;
(2)电荷在磁场中的偏转半径;
(3)电荷第三次到达x轴上的位置。
 在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=
在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E= ×104V/m。x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为 B=1×10-2T。把一个比荷为
×104V/m。x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为 B=1×10-2T。把一个比荷为 C/kg的正电荷从y轴上坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计,求:
C/kg的正电荷从y轴上坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计,求:
(1)电荷从释放到第一次进入磁场时所用的时间t;
(2)电荷在磁场中的偏转半径;
(3)电荷第三次到达x轴上的位置。