(1)图为某介质中一列简谐横波的图像, a、b、为该波上的质点,已知此时a点正沿y轴正向运动,且在1s内完成5次全振动。
①分析从该时刻起a、b两质点那个先回到平衡位确置;
②定波的传播方向和波速。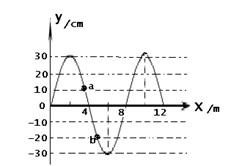
(2)平行光A垂直射向一半径为R的玻璃半球的平面,其截面如图所示。发现只有P、Q之间所对应圆心角为600的球面上有光线射出,则:
①玻璃对光线的折射率
②若仅将平行光A换成B平行光,测得有光线射出的范围增大。设A、B两种光在玻璃球中的速度分别为vA、vB,试比较vA、vB的大小关系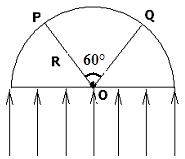
(1)图为某介质中一列简谐横波的图像, a、b、为该波上的质点,已知此时a点正沿y轴正向运动,且在1s内完成5次全振动。
①分析从该时刻起a、b两质点那个先回到平衡位确置;
②定波的传播方向和波速。
(2)平行光A垂直射向一半径为R的玻璃半球的平面,其截面如图所示。发现只有P、Q之间所对应圆心角为600的球面上有光线射出,则:
①玻璃对光线的折射率
②若仅将平行光A换成B平行光,测得有光线射出的范围增大。设A、B两种光在玻璃球中的速度分别为vA、vB,试比较vA、vB的大小关系