如图所示,在虚线AB的左侧固定着一个半径R=0.2m的1/4光滑绝缘竖直轨道,轨道末端水平,下端距地面高H=5m,虚线AB右侧存在水平向右的匀强电场,场强E=2×103 V/m。有一带负电的小球从轨道最高点由静止滑下,最终落在水平地面上,已知小球的质量m=2g,带电量q=1×10-6 C,小球在运动中电量保持不变,不计空气阻力(取g=10m/s2)求: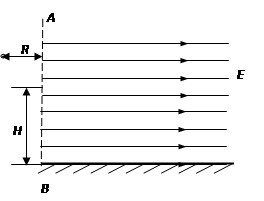
(1)小球落地的位置离虚线AB的距离;
(2)小球落地时的速度。
如图所示,在虚线AB的左侧固定着一个半径R=0.2m的1/4光滑绝缘竖直轨道,轨道末端水平,下端距地面高H=5m,虚线AB右侧存在水平向右的匀强电场,场强E=2×103 V/m。有一带负电的小球从轨道最高点由静止滑下,最终落在水平地面上,已知小球的质量m=2g,带电量q=1×10-6 C,小球在运动中电量保持不变,不计空气阻力(取g=10m/s2)求: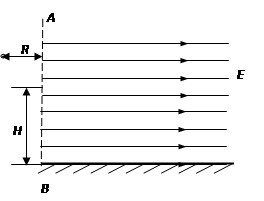
(1)小球落地的位置离虚线AB的距离;
(2)小球落地时的速度。