如图所示,一固定的楔形木块,其斜面的倾角θ=30°,另一边与地面垂直,顶上有一定滑轮.一柔软的细线跨过定滑轮,两端分别与物块A和B连结,A的质量为4m,B的质量为m,开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升.物块A与斜面间无摩擦.设当A沿斜面下滑S 距离后,细线突然断了.求物块B上升离地的最大高度H. 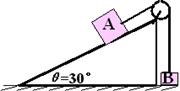
如图所示,一固定的楔形木块,其斜面的倾角θ=30°,另一边与地面垂直,顶上有一定滑轮.一柔软的细线跨过定滑轮,两端分别与物块A和B连结,A的质量为4m,B的质量为m,开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升.物块A与斜面间无摩擦.设当A沿斜面下滑S 距离后,细线突然断了.求物块B上升离地的最大高度H. 