如图所示,水平地面上方分布着水平向右的匀强电场,一“L”形的光滑绝缘硬质管竖直固定在匀强电场中,管的水平部分长L1=0.2m,离水平地面的高度为h=5.0m,竖直部分长为L2=0.1m,一带正电的小球从管的上端口A由静止释放,小球通过管的弯曲部分(长度极短可不计)时没有能量损失,小球受到的电场力大小为重力的一半,空气阻力忽略不计。求:(g=10m/s2)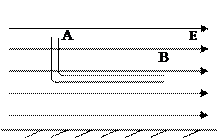
(1)小球运动到管口B时的速度大小;
(2)小球着地点与管的下端口B的水平距离
如图所示,水平地面上方分布着水平向右的匀强电场,一“L”形的光滑绝缘硬质管竖直固定在匀强电场中,管的水平部分长L1=0.2m,离水平地面的高度为h=5.0m,竖直部分长为L2=0.1m,一带正电的小球从管的上端口A由静止释放,小球通过管的弯曲部分(长度极短可不计)时没有能量损失,小球受到的电场力大小为重力的一半,空气阻力忽略不计。求:(g=10m/s2)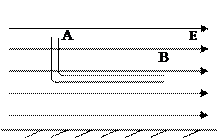
(1)小球运动到管口B时的速度大小;
(2)小球着地点与管的下端口B的水平距离