质量为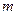 的小球被系在轻绳的一端,在竖直平面内做半径为
的小球被系在轻绳的一端,在竖直平面内做半径为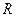 的圆周运动,运动过程中,小球受到空气阻力的作用,设某一时刻小球通过轨道的最低点时,绳子的张力为
的圆周运动,运动过程中,小球受到空气阻力的作用,设某一时刻小球通过轨道的最低点时,绳子的张力为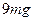 ,此后小球继续作圆周运动,经过半个圆周恰好能通过最高点,则小球从最低点运动到最高点的过程中小球克服空气阻力所做的功为多大?
,此后小球继续作圆周运动,经过半个圆周恰好能通过最高点,则小球从最低点运动到最高点的过程中小球克服空气阻力所做的功为多大?
质量为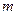 的小球被系在轻绳的一端,在竖直平面内做半径为
的小球被系在轻绳的一端,在竖直平面内做半径为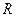 的圆周运动,运动过程中,小球受到空气阻力的作用,设某一时刻小球通过轨道的最低点时,绳子的张力为
的圆周运动,运动过程中,小球受到空气阻力的作用,设某一时刻小球通过轨道的最低点时,绳子的张力为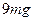 ,此后小球继续作圆周运动,经过半个圆周恰好能通过最高点,则小球从最低点运动到最高点的过程中小球克服空气阻力所做的功为多大?
,此后小球继续作圆周运动,经过半个圆周恰好能通过最高点,则小球从最低点运动到最高点的过程中小球克服空气阻力所做的功为多大?