一个质量为4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1。从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示。(g取10m/s2)求:
①0到2s和2s到4s的加速度。
②83秒内物体的位移大小。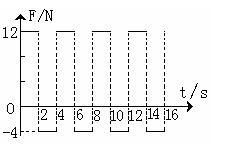
一个质量为4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1。从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示。(g取10m/s2)求:
①0到2s和2s到4s的加速度。
②83秒内物体的位移大小。