某人造地球卫星在赤道平面内沿圆形轨道运行,绕行 方向与地球自转方向相同,轨道半径是
方向与地球自转方向相同,轨道半径是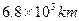 ,周期
,周期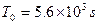 ,
, 。
。
(1)试从这些数据估算地球的质量。(计算结果保留两位有效数字)
(2)已知地球自转周期为T,某时刻该卫星恰在某建筑物的正上方,经多长时间该卫星再一次到达该建筑物的正上方。(不用算数用T0和T表示即可)
某人造地球卫星在赤道平面内沿圆形轨道运行,绕行 方向与地球自转方向相同,轨道半径是
方向与地球自转方向相同,轨道半径是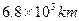 ,周期
,周期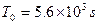 ,
, 。
。
(1)试从这些数据估算地球的质量。(计算结果保留两位有效数字)
(2)已知地球自转周期为T,某时刻该卫星恰在某建筑物的正上方,经多长时间该卫星再一次到达该建筑物的正上方。(不用算数用T0和T表示即可)