如图所示为一空间直角坐标系xoy,在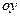 和MN之间的区域内,有宽度为d、沿y轴正方向的匀强电场,电场强度为E。有一质量为m、电量为
和MN之间的区域内,有宽度为d、沿y轴正方向的匀强电场,电场强度为E。有一质量为m、电量为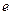 的电子,由静止开始经过另一电势差为U的电场加速后,从
的电子,由静止开始经过另一电势差为U的电场加速后,从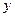 轴上的P点(坐标0、
轴上的P点(坐标0、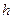 ),沿x轴正方向射入电场(电子重力不计)。
),沿x轴正方向射入电场(电子重力不计)。
(1)求电子能够从x轴上方飞离电场区域,加速电场的电势差U应满足什么条件?
(2)若电子从右边界MN上某点射出后,运动到x轴上的Q点,求Q点的横坐标。(加速电压U已知)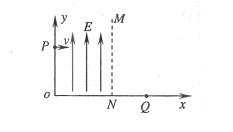
如图所示为一空间直角坐标系xoy,在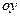 和MN之间的区域内,有宽度为d、沿y轴正方向的匀强电场,电场强度为E。有一质量为m、电量为
和MN之间的区域内,有宽度为d、沿y轴正方向的匀强电场,电场强度为E。有一质量为m、电量为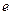 的电子,由静止开始经过另一电势差为U的电场加速后,从
的电子,由静止开始经过另一电势差为U的电场加速后,从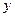 轴上的P点(坐标0、
轴上的P点(坐标0、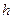 ),沿x轴正方向射入电场(电子重力不计)。
),沿x轴正方向射入电场(电子重力不计)。
(1)求电子能够从x轴上方飞离电场区域,加速电场的电势差U应满足什么条件?
(2)若电子从右边界MN上某点射出后,运动到x轴上的Q点,求Q点的横坐标。(加速电压U已知)