时,磁场在平面内的分布如题23图所示.其磁感应强度的大小均为,方向垂直于平面,相邻磁场区域的磁场方向相反.每个同向磁场区域的宽度均为.整个磁场以速度沿轴正方向匀速运动.
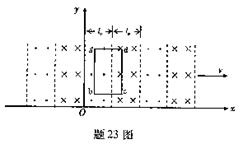
(1)若在磁场所在区间,平面内放置一由匝线圈串联而成的矩形导线框,线框的边平行于轴.、,总电阻为,线框始终保持静止.求
①线框中产生的总电动势大小和导线中的电流大小;
②线框所受安培力的大小和方向.
(2)该运动的磁场可视为沿x轴传播的波,设垂直于纸面向外的磁场方向为正,画出时磁感应强度的波形图,并求波长和频率.
相关知识点
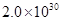 kg。地球质量为
kg。地球质量为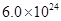 kg,日地距离为
kg,日地距离为 。求太阳和地球间的万有引力大小。(已知
。求太阳和地球间的万有引力大小。(已知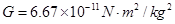 )
)
 、
、 的两个小物块静止在光滑的水平面上,彼此用轻弹簧相连,弹簧处于自由伸长状态。质量为
的两个小物块静止在光滑的水平面上,彼此用轻弹簧相连,弹簧处于自由伸长状态。质量为 的子弹以速度为
的子弹以速度为 水平入射到
水平入射到 物块内(子弹未射出),试求:
物块内(子弹未射出),试求:
 的速度
的速度 的正方形线圈,共100匝,将它置于
的正方形线圈,共100匝,将它置于 的匀强磁场中,绕着垂直于磁场方向的轴以
的匀强磁场中,绕着垂直于磁场方向的轴以 的角速度匀速转动,转动开始时线圈平面与磁场方向垂直,已知线圈的电阻为
的角速度匀速转动,转动开始时线圈平面与磁场方向垂直,已知线圈的电阻为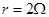 ,外电路的电阻为
,外电路的电阻为 ,试求:
,试求:
 的过程中,通过外电阻R的电量。
的过程中,通过外电阻R的电量。 粤公网安备 44130202000953号
粤公网安备 44130202000953号