图15-5-15是测量带电粒子质量的仪器工作原理示意图，设法使某有机化合物的气态分子导入图中所示的容器A中，使它受到电子束轰击，失去一个电子变成为正一价的分子离子，分子离子从狭缝S1以很小的速度进入电压为U的加速电场区（初速度不计），加速后，再通过狭缝S2、S3射入磁感应强度为B的匀强磁场，方向垂直于磁场区的界面PQ.最后，分子离子打到感光片上，形成垂直于纸面且平行狭缝S3的细线.若测得细线到狭缝S3的距离为d.导出分子离子的质量m的表达式.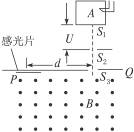
图15-5-15
图15-5-15是测量带电粒子质量的仪器工作原理示意图，设法使某有机化合物的气态分子导入图中所示的容器A中，使它受到电子束轰击，失去一个电子变成为正一价的分子离子，分子离子从狭缝S1以很小的速度进入电压为U的加速电场区（初速度不计），加速后，再通过狭缝S2、S3射入磁感应强度为B的匀强磁场，方向垂直于磁场区的界面PQ.最后，分子离子打到感光片上，形成垂直于纸面且平行狭缝S3的细线.若测得细线到狭缝S3的距离为d.导出分子离子的质量m的表达式.
图15-5-15
粤公网安备 44130202000953号