德布罗意认为,任何一个运动着的物体,都有一种波与它对应,波长是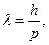 式中p是运动物体的动量,h是普朗克常量.已知某种紫光的波长是440 nm,若将电子加速,使它的德布罗意波长是这种紫光波长的10-4倍,求:
式中p是运动物体的动量,h是普朗克常量.已知某种紫光的波长是440 nm,若将电子加速,使它的德布罗意波长是这种紫光波长的10-4倍,求:
(1)电子的动量的大小.
(2)试推导加速电压跟德布罗意波长的关系,并计算加速电压的大小.电子质量m=9.1×10-31 kg,电子电荷量e=1.6×10-19 C,普朗克常量h=6.6×10-34 J·s,加速电压的计算结果取一位有效数字.
德布罗意认为,任何一个运动着的物体,都有一种波与它对应,波长是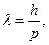 式中p是运动物体的动量,h是普朗克常量.已知某种紫光的波长是440 nm,若将电子加速,使它的德布罗意波长是这种紫光波长的10-4倍,求:
式中p是运动物体的动量,h是普朗克常量.已知某种紫光的波长是440 nm,若将电子加速,使它的德布罗意波长是这种紫光波长的10-4倍,求:
(1)电子的动量的大小.
(2)试推导加速电压跟德布罗意波长的关系,并计算加速电压的大小.电子质量m=9.1×10-31 kg,电子电荷量e=1.6×10-19 C,普朗克常量h=6.6×10-34 J·s,加速电压的计算结果取一位有效数字.