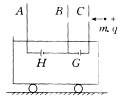
如图所示，三块平行金属板竖直固定在绝缘小车上，并与车内电池连接，小车总质量为M，静止在光滑水平面上，金属板B、C中间开有小孔，两孔在同一水平线上，已知车内电池G的电动势为 E1，现有一质量为m，带电量为q的粒子(不计重力)，以初速
，水平射入C板小孔，它穿过B板小孔后继续向A板运动。
①为使粒子不至打到A板上，电池H的电动势E2应满足什么条件?
②若A、B、C间隔均为d，满足上面条件的电池H的电动势用E2表示，则当小车运动后，其速度大小具有最小值时，带电粒子离B板的距离是多大?
如图所示，三块平行金属板竖直固定在绝缘小车上，并与车内电池连接，小车总质量为M，静止在光滑水平面上，金属板B、C中间开有小孔，两孔在同一水平线上，已知车内电池G的电动势为 E1，现有一质量为m，带电量为q的粒子(不计重力)，以初速，水平射入C板小孔，它穿过B板小孔后继续向A板运动。
①为使粒子不至打到A板上，电池H的电动势E2应满足什么条件?
②若A、B、C间隔均为d，满足上面条件的电池H的电动势用E2表示，则当小车运动后，其速度大小具有最小值时，带电粒子离B板的距离是多大?
粤公网安备 44130202000953号