一质量为m、带电量为+q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴,速度方向与x轴正方向的夹角为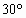 ,同时进入场强为E、方向沿与x轴负方向成
,同时进入场强为E、方向沿与x轴负方向成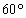 角斜向下的匀强电场中,通过了b点正下方的c点.如图所示,粒子的重力不计,试求:
角斜向下的匀强电场中,通过了b点正下方的c点.如图所示,粒子的重力不计,试求:
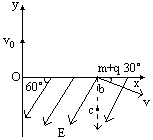
(1)圆形匀强磁场区域的最小面积:
(2)c点到b点的距离.
一质量为m、带电量为+q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴,速度方向与x轴正方向的夹角为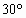 ,同时进入场强为E、方向沿与x轴负方向成
,同时进入场强为E、方向沿与x轴负方向成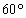 角斜向下的匀强电场中,通过了b点正下方的c点.如图所示,粒子的重力不计,试求:
角斜向下的匀强电场中,通过了b点正下方的c点.如图所示,粒子的重力不计,试求:

(1)圆形匀强磁场区域的最小面积:
(2)c点到b点的距离.