如图所示,一个质量为m,电阻为R的闭合矩形线圈,长为l,高为h,从某一高度由静止开始下落,进入一个有界匀强磁场区域,磁场方向垂直纸面向里,磁感应强度大小为B,磁场的边界为水平,宽度为2h,线圈开始下落时距磁场上边界3h,下落过程中始终在竖直平面内,不发生转动.已知线圈从磁场中穿出的过程中,做的是匀速运动.求线圈在进入磁场的过程中有多少电能转化为内能?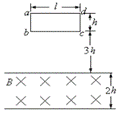
如图所示,一个质量为m,电阻为R的闭合矩形线圈,长为l,高为h,从某一高度由静止开始下落,进入一个有界匀强磁场区域,磁场方向垂直纸面向里,磁感应强度大小为B,磁场的边界为水平,宽度为2h,线圈开始下落时距磁场上边界3h,下落过程中始终在竖直平面内,不发生转动.已知线圈从磁场中穿出的过程中,做的是匀速运动.求线圈在进入磁场的过程中有多少电能转化为内能?