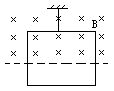
如图所示，一个边长为L的正方形金属框，质量为m，电阻为R ．用细线把它悬挂于一个有界的磁场边缘。金属框的上半部处于磁场内，下半部处于磁场外。磁场随时间均匀变化满足B=kt规律。已知细线所能承受的最大拉力T=2mg．求从t=0时起，经多长时间细线会被拉断。