如图所示,一根对称的A形玻璃管置于竖直平面内,管所在的空间有E=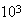 V/m、方向向下的匀强电场,重力G=1.0×
V/m、方向向下的匀强电场,重力G=1.0× N,电荷量为-2.0×
N,电荷量为-2.0×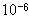 C的小物体m在管内从A点由静止开始运动,m与管壁的动摩擦因数为0.5,管长AB=BC=2m,管的B处为一极短的光滑圆弧,管AB、BC与水平方向的夹角均为37°,(g取10m/
C的小物体m在管内从A点由静止开始运动,m与管壁的动摩擦因数为0.5,管长AB=BC=2m,管的B处为一极短的光滑圆弧,管AB、BC与水平方向的夹角均为37°,(g取10m/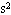 ) 问:
) 问: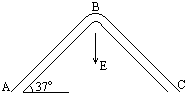
(1)m达到最高点时的速度多大?
(2)m从A点开始运动到第一次速度为零的位置在何处?
(3)从A开始运动,到最终停下来总路程为多大?
相关知识点
如图所示,一根对称的A形玻璃管置于竖直平面内,管所在的空间有E=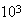 V/m、方向向下的匀强电场,重力G=1.0×
V/m、方向向下的匀强电场,重力G=1.0× N,电荷量为-2.0×
N,电荷量为-2.0×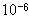 C的小物体m在管内从A点由静止开始运动,m与管壁的动摩擦因数为0.5,管长AB=BC=2m,管的B处为一极短的光滑圆弧,管AB、BC与水平方向的夹角均为37°,(g取10m/
C的小物体m在管内从A点由静止开始运动,m与管壁的动摩擦因数为0.5,管长AB=BC=2m,管的B处为一极短的光滑圆弧,管AB、BC与水平方向的夹角均为37°,(g取10m/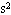 ) 问:
) 问:
(1)m达到最高点时的速度多大?
(2)m从A点开始运动到第一次速度为零的位置在何处?
(3)从A开始运动,到最终停下来总路程为多大?